A Junior Quant's Guide to Hedging

Too much risk in your options book? Here's how to dump it... sort of.

The O’Hare Hedge (n.) — When a trader from Chicago hedges a massive position with a plane ticket out of O’Hare airport. If the trade goes well, great — if it doesn’t, their best option is to head to the airport and start a new life.

An extreme example, but one that highlights one of the toughest challenges in modern finance. As traders, we wish to make the most possible when times are good and lose the least when times are bad — as a result, hedging has become a commonplace practice within the industry.

Today, we’ll do a quick dive into some real-world quantitative hedging techniques across alternative and traditional markets. We’ll cover concepts ranging from optimal hedging structures to inherent tradeoffs.

So, without further ado, let’s get into it!

Alternative Hedging

In the 21st century, there are all manners of inventive financial contracts, so there’s no need to limit ourselves to just the traditional forms.

To get started, let’s first outline the scenario we need to hedge for:

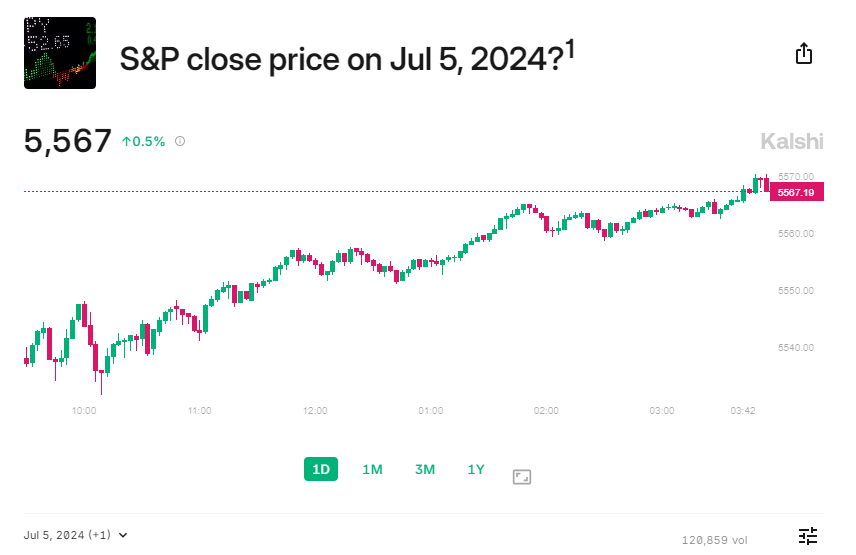
• Our core strategy sells 0-DTE credit spreads.

  • During bull markets we generally sell puts, so our main risk factor comes from negative changes in the underlying price (i.e., if SPX goes down, we lose money). We wish to hedge against the possibility of SPX falling below our short strike.

To do this, we’ll first step outside of conventional options and head over to Kalshi, an event prediction market. As we’ve covered previously, there are a whole heap of niche markets that can be profitably traded:

Prediction Markets Are Literally Free Money. [Code Included]

However, there’s one particular market that’s right up our alley:

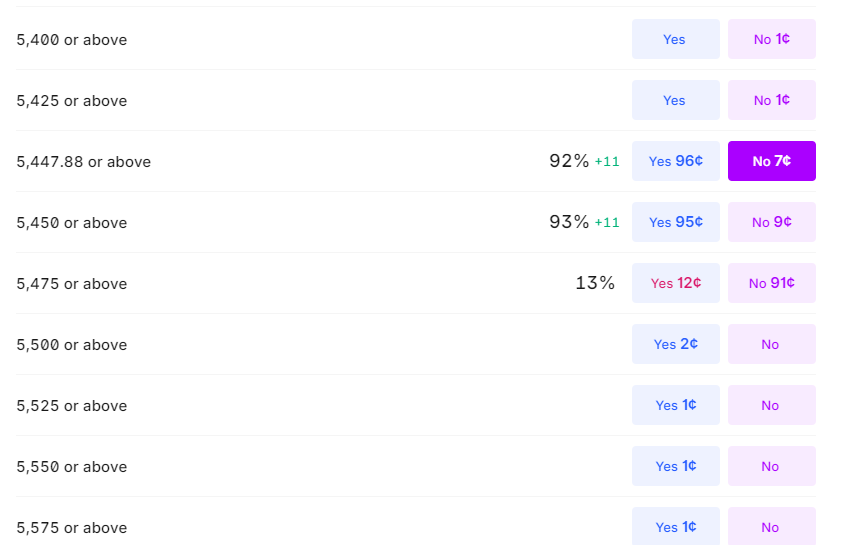
The S&P Above/Below market allows us to take wagers on whether or not SPX will close above the contract-specified value. If say, we held the “5500 or above” contract, the “Yes” contract would mature at $1 if it closes above 5500, and the “No” contracts would expire worthless.

To see why this payout structure is extremely beneficial to us, let’s walkthrough an example:

1. At market open we short the 5500 put and buy the 5495 put. If the price of SPX closes below 5500 (our short strike), we will lose money. For this trade, we collect a premium of $100 for a maximum loss of $400.

2. We want to buy an insurance contract that makes at least $400 if SPX goes below 5500, this way if we end up taking the max loss on the options position, we just get back to even when the insurance contract kicks in.

   1. To do this, we head to Kalshi and select the “No” wager for the “5500 or above” contract. This contract will resolve to $1 if SPX does not close above 5500 or in other words, it pays off if it closes below our short strike.

Simple enough — a good clean hedge. However, there’s a problem.

The price we pay to flatten our risk changes based on the market’s implied probability of the event occurring. If the markets deem it likely that SPX will close below our short strike, the cost of hedging can exceed the premium collected which would lock-in a loss.

Here’s what that might look like:

1. We collect $100 in premium and want to hedge the $400 of risk.

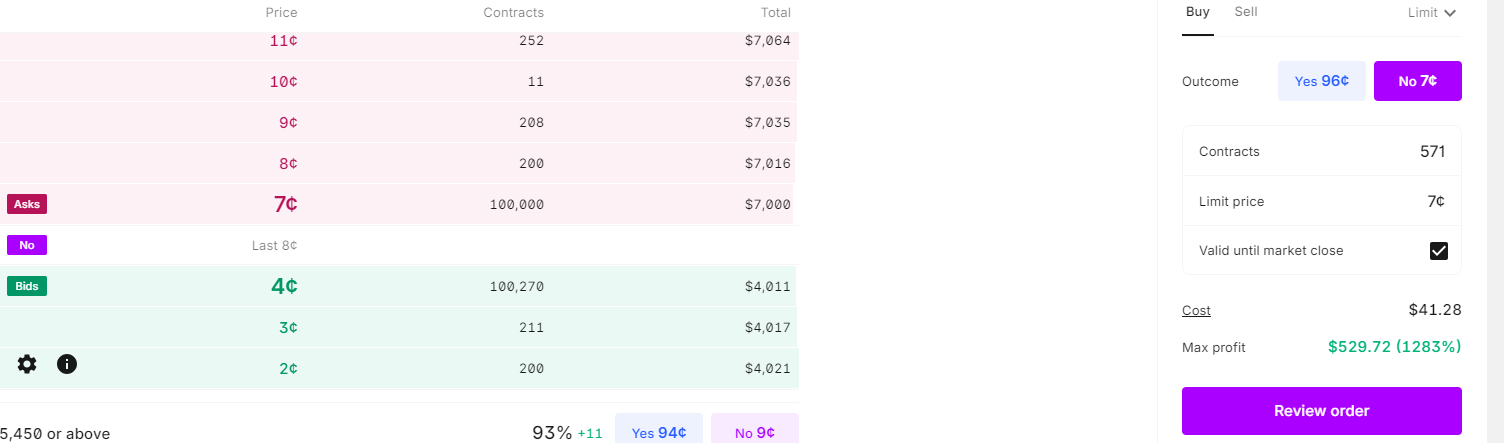
2. The cost of the hedging contract is $.52.

   1. If the contract pays off, it will generate $0.48 per contract at expiration (1-.52).

   2. To hedge our risk (make $400 in the event of a payoff) we need to buy 834 contracts (834*.48 = ~400).

   3. The cost for 834 contracts will be $433 (834 *.52).

3. If the contract pays off, we lose $400 on the option position, but we make $400 on the contract to end the day flat. However, if it doesn’t payoff (our base case), we make $100 on the option position, but lose $433 on the insurance contract, to end the day at a loss.

   

So, to solve this problem, we need to purchase the insurance contract at a price that still allows us to end with a profit if we end up not needing it:

As the trading session goes on and the probability of an insurance payoff decreases, so does the price of the contract. Additionally, there is generally a good bit of liquidity across the market:

So, from here we can devise a hedging strategy:

1. Each morning we sell our standard spread

2. We wait until the price of hedging is less than or equal to 10% of our collected premium.

   1. This way, even if the hedge doesn’t payoff, we still keep 90% of our profits.

3. If the price never reaches that point, we remain unhedged.

Let’s pull some data and run a backtest to see if the scheme would’ve helped us out: